Morphing
Morphing is a type of vortex movement of which already plenty of examples have been shown on the preceding pages. The sum vortex movement, thus the normal flow movement of a vortex, is one way that expansion or contraction can progress from one vortex in the sequence to another vortex in the sequence (when two vortices are connected). Morphing is another way that this can happen. Vortices can change into other types of vortices by gradually changing from one shape to another. It happens to be that spirals can change into subsequent spirals and ladders can change into subsequent ladders. This change in appearance from one vortex type to another is what I chose to call 'morphing'.

Morphing happens when the dimensionality level of a vortex as a whole increases or decreases. The vortex thereby changes from one vortex type to another, and thereby changes its shape and appearance. Or sometimes the vortex remains in a intermediate state between the two vortex types. Morphing is caused by a change direction that the wave travels in the onefield, the wave that travels from the onefield onto, and pass our physical world, and that thereby creates a vortex at the position where our physical world is crossed by the wave. A change in direction of the wave result in an increase or decrease in the number of dimensions that are projected onto our physical world. Thus the wave appears to have become higher (more yin) or lower (more yang) dimensional. One way in which this manifests to our perception is that the properties of the wave change in frequency and wavelength. If we humans would live outside of the so called 'physical plane' (which was mentioned on the page titled 'The Great Puzzle'), and if we then would be able to 'see' all the dimensions are they are without anything being hidden for us, then we would see only see waves that all travel at the same speed, with equal wavelengths (but changes are that there are more ways in which those waves will manifest themselves differently to us then they do now).
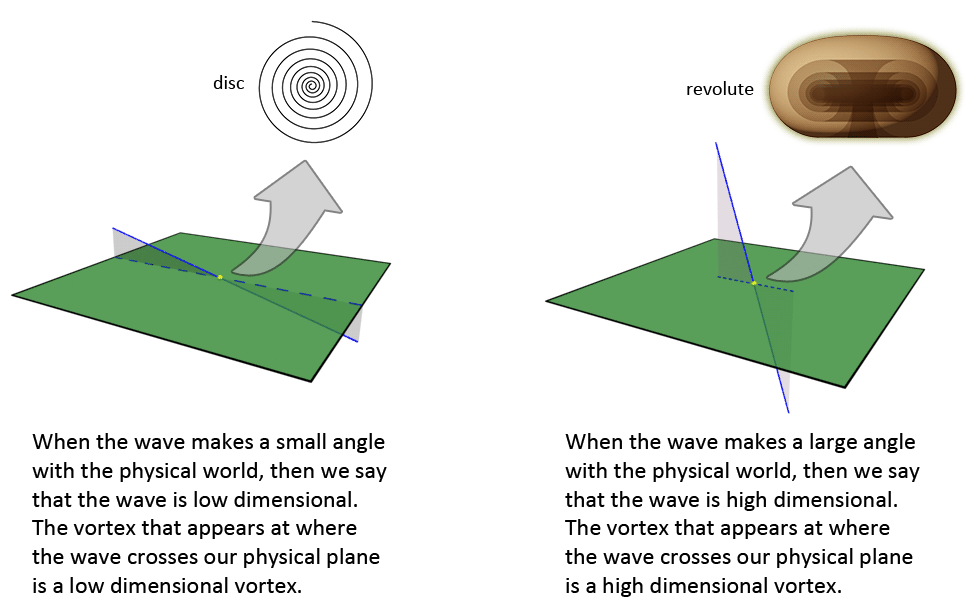
During morphing, the trajectories of the meridians change, and the number of meridians change. Each type of vortex can morph into a different type of vortex two dimension levels higher or two dimension levels lower in the sequence. Vortices thus change into a subsequent vortex of the same class. This holds true for all the vortex types. The step size is always two dimensions, but the class type is not always identical. The change of a vortex's class during morphing is a consequence of passing a transitional mirror point while morphing. A mirror point can for example be an EM crossing location, like the zero point or the infinity ring. Or it can be a central balance point in any of the half-cycles. When an outer bridge vortex for example crosses the main balance point due to morphing, its class changes from outer bridge to inner bridge.
At the main central balance point, outer bridges change into inner bridges, and inner bridges change into outer bridges. But ladders remain ladders, spirals remain spirals, and tunnels remain tunnels. Same holds true for the zero point and the infinity ring (EM crossing locations).
Downward Morphing and Upward Morphing
Downward morphing is when a vortex changes shape by transforming into a lower dimensional vortex. Upward morphing is when a vortex changes shape by transforming into a higher dimensional vortex. All observed morphing so far has been upward morphing, downward morphing has not yet been observed. Upward morphing always goes along with an increase of scale size. The vortices grow while morphing. For all vortices below the central balance point this might seem logical, because those vortices, as they are connected in the sequence, rapidly become larger with the increase of the dimensionality level. But above the central balance point, the vortices become smaller in the connected sequence, but become larger when morphing upwards. A vortex that morphs into a smaller vortex has not yet been observed.
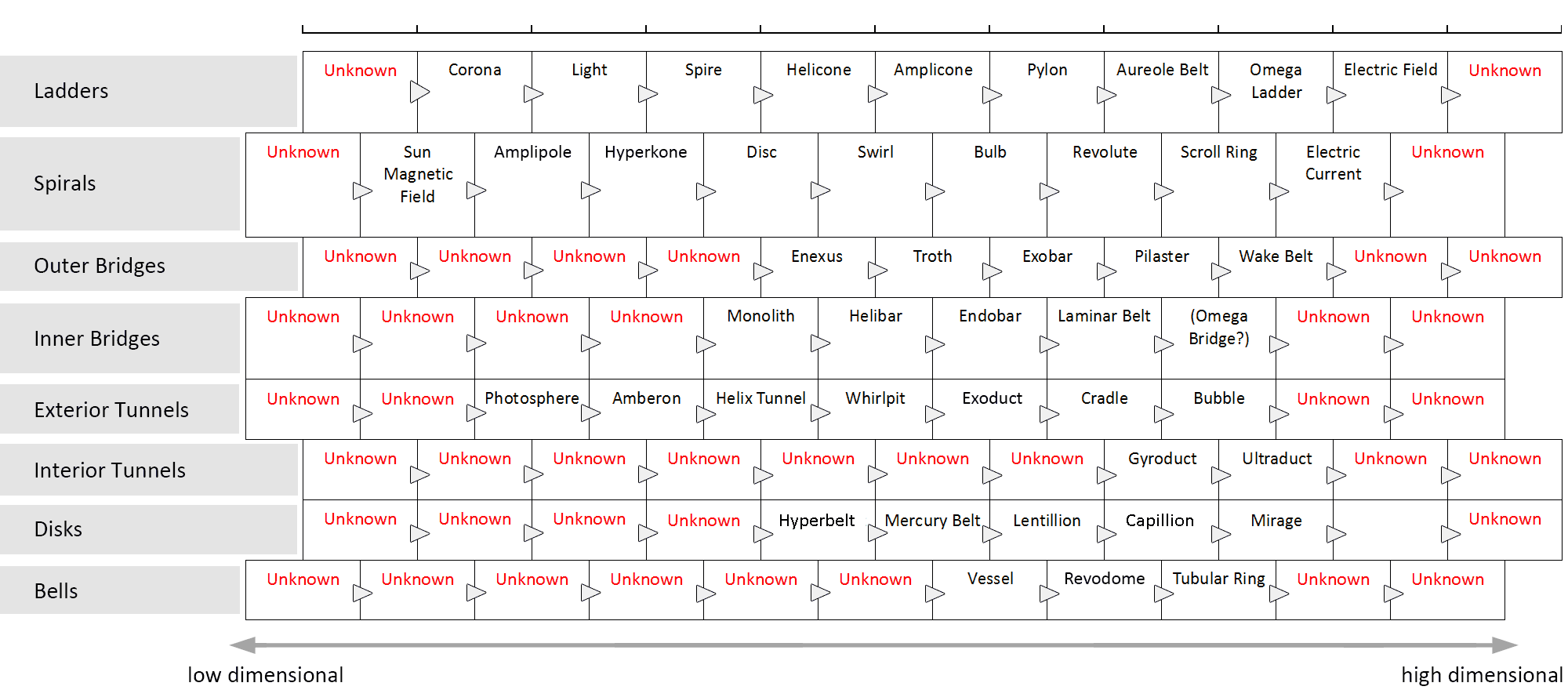
The image below shows a chart with all the known morph sequences so far (from left to right). You can click on the image for a larger view of the chart.
Terminology
When a vortex is not morphed we say that that vortex is an unmorphed vortex. So you can have an unmorphed spire, an unmorphed disc, an unmorphed helicone etc. In that condition the vortex shape looks much like the basic shape of that vortex type (but there can be other factors that alter its appearance). That a vortex is morphed does not mean that it's morphing. A vortex can retain in the same morphed state for a while without morphing further. Some vortices move so slow, that we do not know for sure if they're morphing, like many of the observations from Hubble space telescope.
When a vortex is partially morphed into another vortex then we say that that vortex is morphed. The vortex looks like an intermediate state between two basic vortex types. Another way to say that that vortex is morphed is by calling it a highmorph vortex or a lowmorph vortex. This gives us more information about how much the vortex is morphed. Yet another way of saying it is by using the words upmorph and downmorph. Both these terms have already been mentioned on the page titled 'Vortices and Dimension Levels'. Here I'll briefly explain them again.
For example, when a vortex is an intermediate state of a spire and a helicone, then we say that that vortex is a highmorph spire if its shape is closer to that of a spire, and we call it a lowmorph helicone if that shape is closer to that of a helicone. When a vortex is a highmorph spire, and we also know that the vortex has morphed from an unmorphed spire to a highmorph spire, then we can also say that the vortex is an upmorphed spire. That way we add some information about the direction of movement. In a similar way, when a vortex is a lowmorph helicone, and we also know that the vortex has morphed from an unmorphed helicone to a lowmorph helicone, we can say that the vortex is a downmorphed helicone.
Morphing Ladders
Below are some examples of ladder vortices that morph into a subsequent ladder, which is in all cases two dimension levels higher than the first. These examples are all vortices from the first half-cycle.
Spire Morphing into a Helicone
(from the 1st dimension level to the 3rd dimension level)
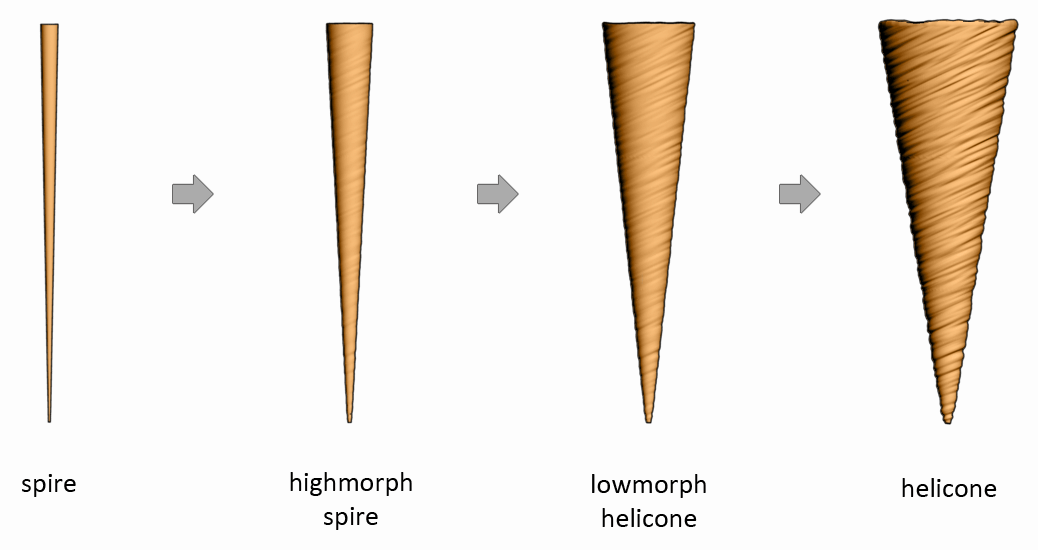
Helicone Morphing into an Amplicone
(from the 3rd dimension level to the 5th dimension level)
![]()
Amplicone Morphing into a Pylon
(from the 5th dimension level to the 7th dimension level)
![]()
Pylon Morphing into an Aureole Belt
(from the 7th dimension level to the 9th dimension level)

At some nuclear detonations we can see an aureole belt morphing into an omega ladder. The aureole belt has a horizontal cross-section (thus its shape is annular), but the omega ladder has a vertical cross-section (thus its shape is like a very short cylinder). When the aureole belt morphs into an omega ladder, its shape becomes curved, and eventually makes a full 90 degree turn before fully becoming an omega ladder. Below you see a video of one such morphing taking place (it takes place in the first seconds of the explosion).
This ladder vortex was the last morphing ladder within the first half-cycle. So now I've shown all the steps of morphing for the ladders within one half-cycle. Putting all these steps together results in the following animation.
Morphing Spirals
This same morphing also happens with the spirals. Every spiral in the sequence can morph into a subsequent spiral. Here too the second vortex is two dimension levels higher than the first. And here too I'll show a few examples.
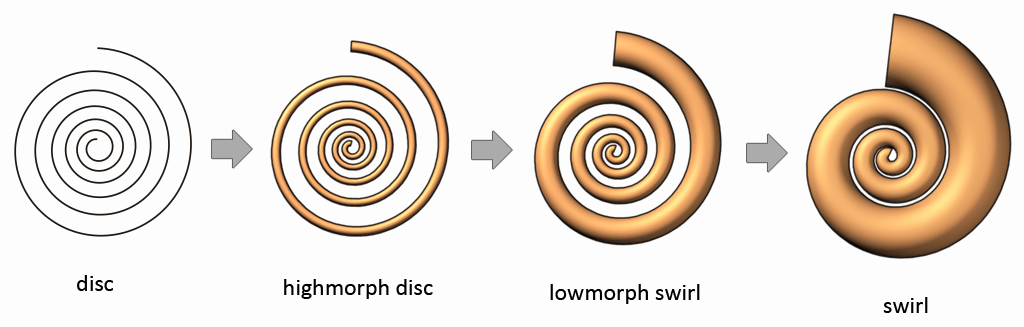
Disc Morphing into a Swirl
(from the 2nd dimension level to the 4th dimension level)
Swirl Morphing into a Bulb
This puzzle piece was the hardest one to find. Because the bulb lies at the center of the sequence, it morphs in a different way than the other spirals.
When a swirl morphs into a bulb, then the center of the swirl expands and the bulb forms itself at the center between the inner ends of the two spiral arms while the helibars and helicones slowly get absorbed and become part of the growing bulb. At that same time the spiral arms get shorter and shorter because the spiral keeps expanding at the center.
 Image by NASA, ESA, and The Hubble Heritage Team STScI/AURA). Image was cropped and rotated 18° CCW. |
 Bulb forming at the center of a swirl |
This kind of morphing can best be seen with spiral galaxies, which often form a bulb at the center of the galaxy in the location where the spiral bar is located. This vortex overlaps the spiral bar, which disappears as the bulb further forms itself.
The above left drawing is not correct yet. It only shows the helicones but I still need to add the straight helibars next to the conical helicones. But the correct image is already observable in barred spiral galaxies. Some galaxies show the bulb and spiral bar very clearly.
Rattleback
A man-made object that works on the same principles as the center of a morphing spiral galaxy, a bar with two ladders, is a toy called the rattleback. A rattleback is a semi-ellipsoidal spinning toy that prefers to rotate in one direction. If spun in the other direction, then it will come to a standstill after the spin becomes unstable, and then it rotates back in the preferred direction. This spin-reversal appears to violate the law of the conservation of angular momentum, and makes the rattleback a physical curiosity that has excited human imagination since prehistorical times.

Screenshot taken from video by Z Corporation. Image was edited with text and lines
The reason that it works is because this toy mimics the same vortices that are present within the center of a spiral galaxy as in the previous image. The shape of a rattleback is that of a lowmorph double bulb cut in half along its length axis. The hollow compartments in the photo above are where the spiral arms are located. They are oriented this way in a spiral galaxy because both these ladders meet the outer ends of one disc spiral at the center, for that these ladders can not meet each other head on, instead they are positioned closer to the edge of the double bulb, one for each side.
The photo above shows one type of rattleback, but there are several types that effectively work as toys that only want to rotate in one direction. The video below shows another type of rattleback. This one only works by mimicking the connections of the spiral arms, which in this case is how the two turtles are positioned and oriented.
It could be that this little toy reveals to us that spiral galaxies that have a spiral bar with ladders do not only flow but do also rotate. And the obvious reason why this toy works the way it does is for the same reason that a spiral galaxy only rotates in one direction, depending on whether its a left-turning or right-turning swirl. It can not be both at the same time. More needs to be found out to come to a conclusion, but this could be an important discovery for astronomy.
Bulb Morphing into a Revolute
(from the 6th dimension level to the 8th dimension level)

Here you have two different examples of a bulb morphing into a revolute. I do not know the source of the upper image, so I do not know the description of the mediums that were used. The video below is a plume driven by a chemical reaction. The plume accelerates and sheds accelerating smoke ring vortices.
 |
Revolute Morphing into a Scroll ring
(from the 8th dimension level to the 10th dimension level)
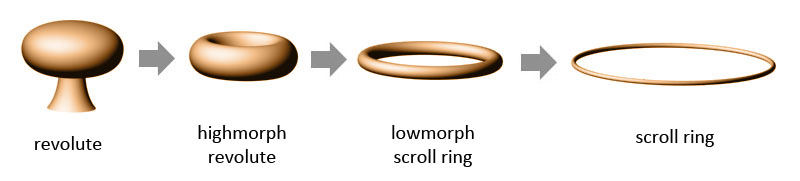
The first image on the left shows a revolute with a pylon. I added the pylon so that you can see that it's a revolute (I should instead have drawn the revolute better, its shape is not entirely correct. I still need to change that).
It is not hard to tell if a revolute is somewhat morphed towards a scroll ring or not. An unmorphed revolute always has a closed roof, from the outside you cannot see the ring shape unless its sufficiently transparent to see the inner structure. As soon as the revolute has a hole in its roof you know that it has morphed. From then on it quickly changes into a ring/donut shape.
A scroll ring that is unmorphed is a very thin ring. It is not easy to determine whether a scroll ring is completely unmorphed. An important detail is that the scale of the vortex ring increases as it morphs to a scroll ring. It could be that the same also happens with the other vortices in the sequence when they morph. But there are not enough observations of morphing to confirm whether this is true.
The videos below show another two examples of a revodome morphing into a tubular ring, one in water and one in air (as smoke). The smoke ring might be a revolute morphing into a scroll ring instead of a revodome morphing into a tubular ring. A smoke ring can be either those types and the difference is not always easy to determine.
Morphing Outer Bridges
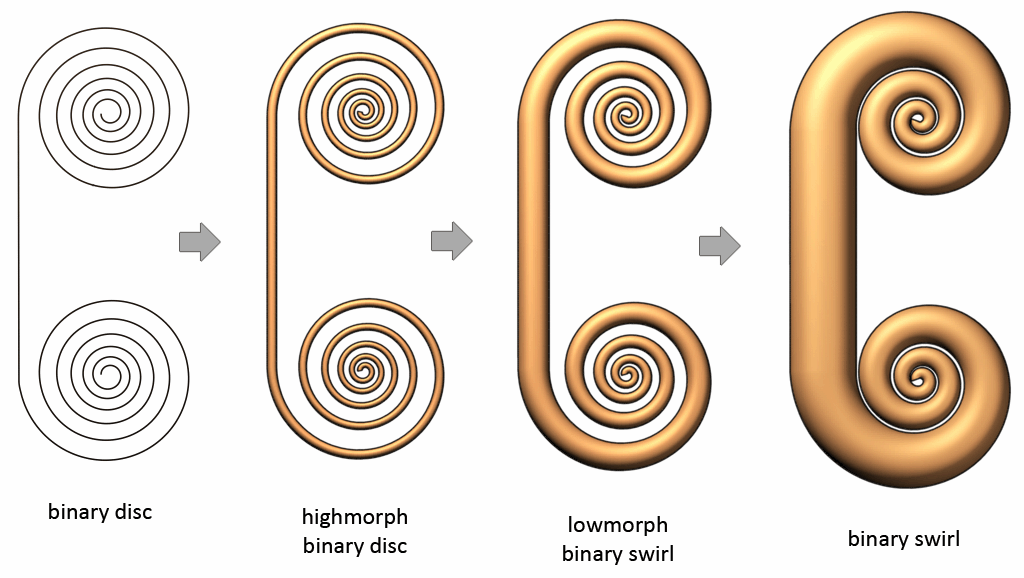
Just as single spirals can morph into subsequent single spirals and double spirals can morph into subsequent double spirals, so can a binary spiral morph into a subsequent binary spiral, thus thereby morphing an outer bridge in a subsequent outer bridge.
Binary Disc Morphing into a Binary Swirl
(from the 2nd dimension level to the 4th dimension level)
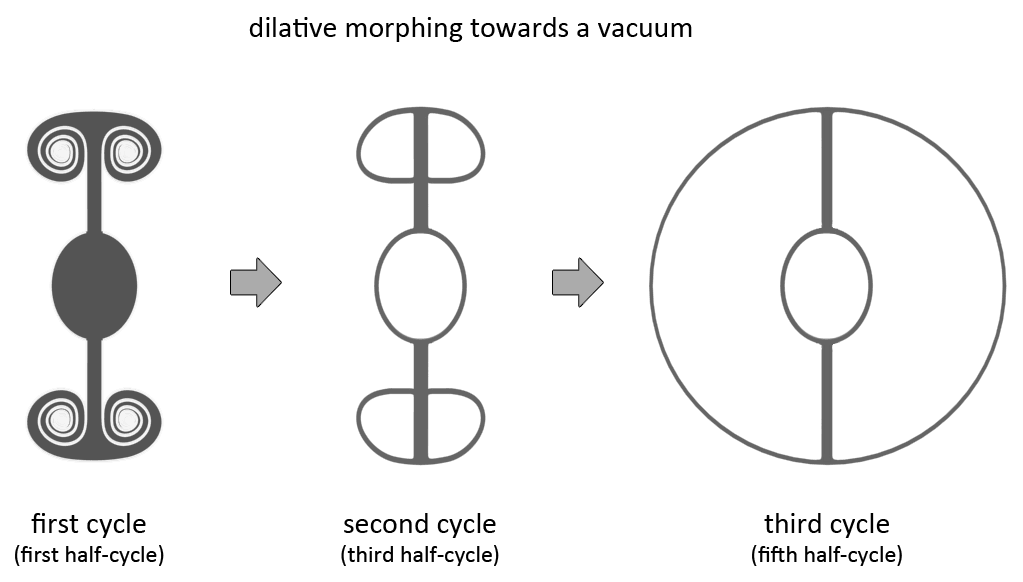
Dilative Morphing
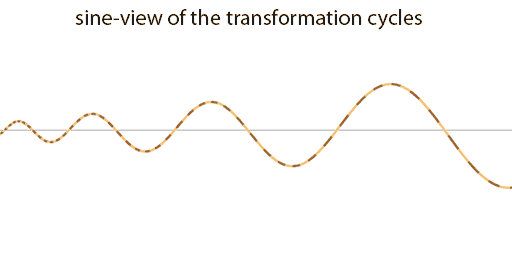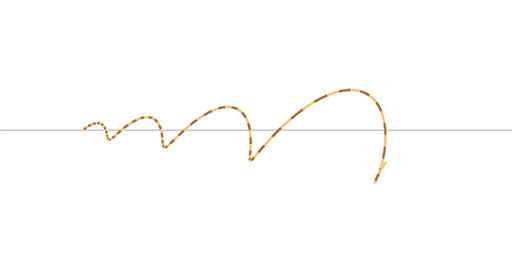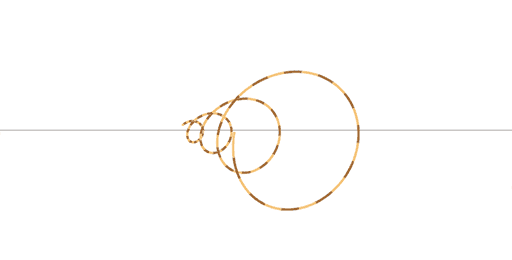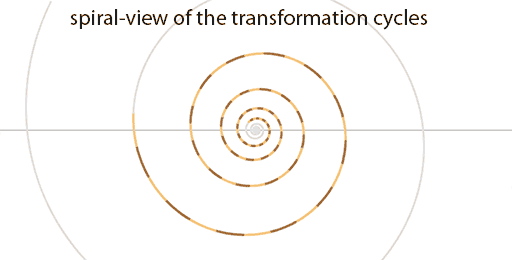
While sequential morphing is the gradual transformation of a vortex into the next vortex of the same class within the same cycle, dilative morphing is the gradual transformation of a vortex to the vortex that is most close by within the next cycle. In what direction this movement takes place within the transformation sequence is shown below. The image shows the different cycles of the transformation sequence laid out in a spiral, one rotation of the spiral is one cycle in the sequence. Movement along the direction of the spiral is called sequential morphing, the vortex morphs into the next vortex in the sequence of the same class (two dimension levels higher at a time). All the previous examples of morphing on this page are sequential morphing examples. Movement from one cycle to the next is called dilative morphing, which is a whole different type of morphing.
For the first half-cycle, dilative morphing implies that spirals morph into disks or bell vortices. The vortex thereby makes a movement from the first half-cycle to the third half-cycle (and thus from the first cycle to the second cycle).
What shape a spiral vortex becomes that dilates is simple to predict. The movement of the spiral moves to its extremities, the vortex dilates. The new vortex looks much like a hollow version of the first cycle, and there is no longer an increase or decrease in dimensionality level within the movement of the vortex. The vortex no longer has two ends that both differ in dimensionality level. Instead the vortex loops onto itself. Much like in the two examples shown above and below, of the swirl and the revolute.
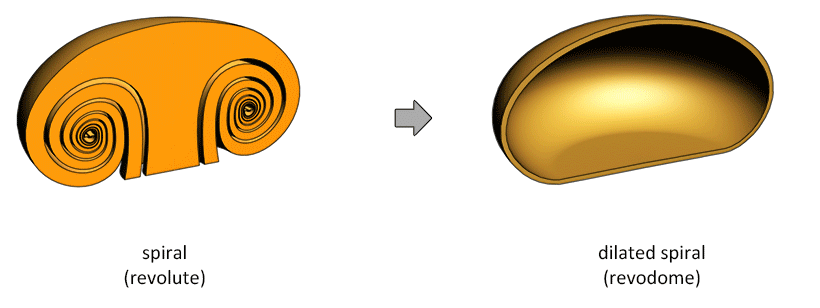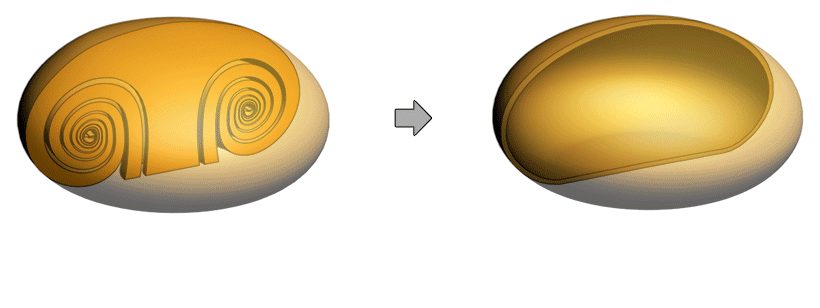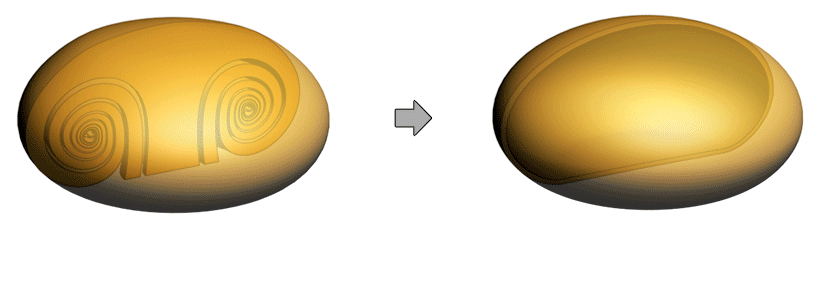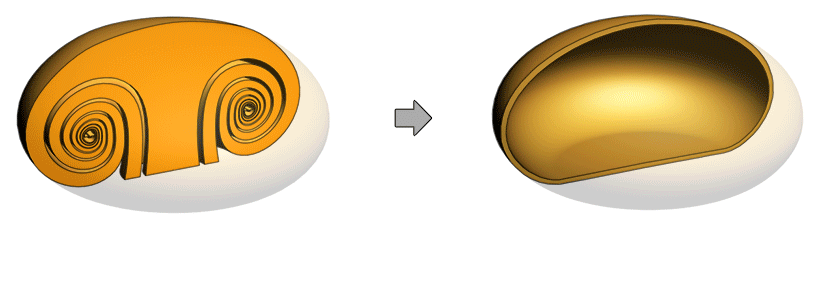
A dilated spiral in some cases looks much the same as its former version, the undilated spiral. Smoke and bubble rings can easily be mistaken for revolutes and scroll rings because they both look similar in outer shape to revodomes and tubular rings. But revodomes and tubular rings lack the inner windings. Sometimes a vortex can be a intermediate state between a spiral and a dilated spiral, in that case it has windings to some degree. Bubble rings never appear to have inner windings. But smoke rings sometimes do and sometimes do not. The photo below shows smoke rings that form from the ignition of a lighter. It also shows the revodome morphing into a tubular ring. To some degree the rings do appear to have windings. To some degree the vortex is in an intermediate state between the first half-cycle and the third half-cycle.
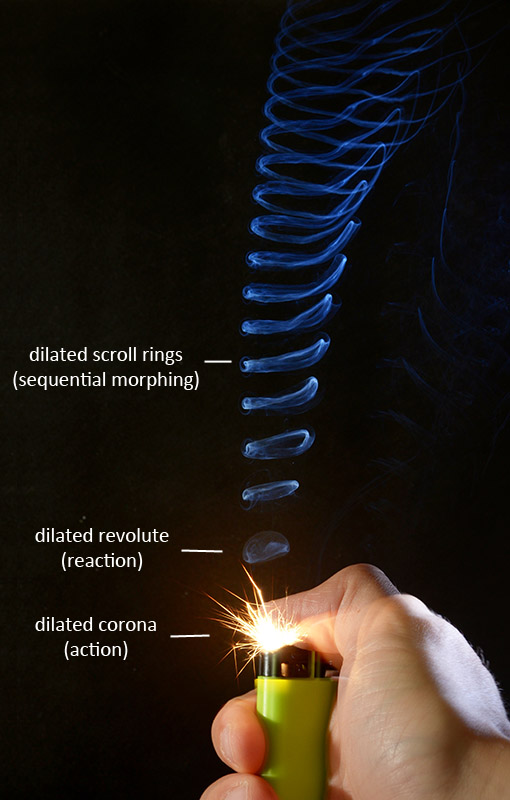
Image by Simon A. Eugster (Wikimedia), under
CC BY-SA 3.0 license. Image was edited with
text, lines, canvas size and contrast.
You should be aware that there are different types of smoke, and different types of smoke have different properties. Smoke from cigarettes is higher dimensional than the smoke from a wood fire. And it appears that smoke from cannabis is even higher dimensional. One can make beautiful vortices in complex shapes from the smoke of a cigarette, which are not easy to produce in most other mediums.
Vacuums
The word vacuum comes from Latin, meaning 'an empty space, void'. Vacuum is a region of space in which no atoms can be detected. Something that comes close to that is a region with a very low gaseous pressure, much less than the atmospheric pressure. Such vacuums might be created in a laboratory and are called 'partial vacuums'. A perfect vacuum is a theoretical concept which has never been achieved and is believed to be impossible.
The outer space has very low density and pressure, and is close to being a perfect vacuum. Still no vacuum is a perfect vacuum, and even the interstellar space has a few hydrogen atoms per cubic meter.
One way to create a vacuum at home is with a suction cup. If you press a section cup flat against a surface and pull it back, a vacuum will form inside the suction cup. This vacuum is the reason for why the cup sticks to the surface. If you make the syringe airtight by closing up the hole at the end of the syringe and the pull back the plunger, a vacuum will form itself inside the syringe.
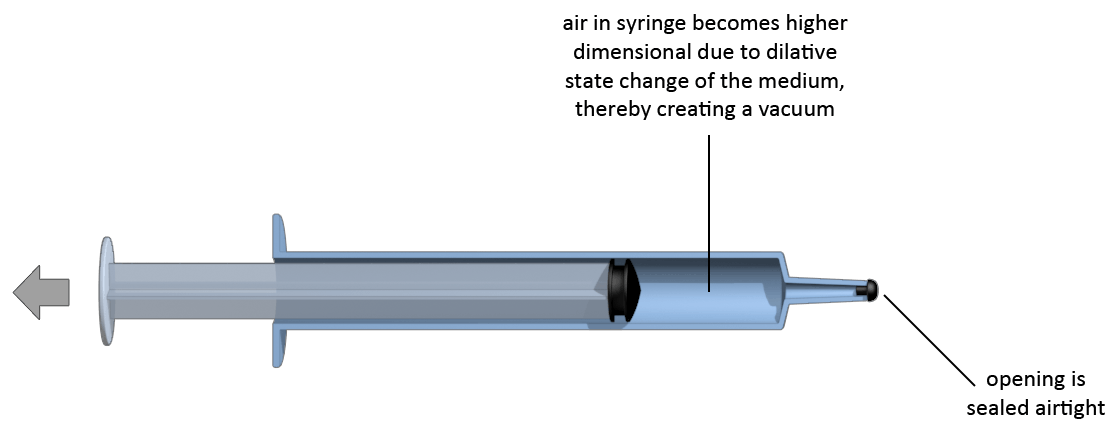
The state of equilibrium for a high vacuum are the vortices within the fifth half-cycle (third cycle), and the vortices within the third half-cycle form low vacuums. It are the suprabells that form vacuums. A vacuum is formed by one state of equilibrium. Metals are also formed by the suprabells, but they have more than one state of equilibrium.
The number of meridians in the vortices within the third half-cycle is much higher than the number of meridians in the fifth half-cycle. And in the fifth half-cycle the number of meridians is again much higher than in the third. This great increase in the required number of meridians for a vortex is the reason why a suction cup can produce so much force. By pulling the air apart dilative morphing takes place, but the movement is incorrect. A suction cup or a syringe pulls the air in only one direction, along one axis. For the movement to be correct the air would need to be pulled apart in three directions simultaneously. Because of this wrong movement the number of meridians of the medium stays the same, while the number of required meridians becomes larger. This creates strong tension that prevents the movement from going further.
THE REASON THAT IT TAKES SO MUCH FORCE TO PULL AIR APART IS BECAUSE THAT MOVEMENT IS DILATIVE MORPHING WITHOUT INCREASE OF NUMBER OF MOVEMENTS (MERIDIANS). THE NUMBER OF REQUIRED MOVEMENTS IN THE NEXT CYCLE IS MUCH HIGHER, THUS THE ATTEMPTED MOVEMENT CREATES VERY STRONG TENSION.
I'm not sure if pulling apart air along all three axes simultaneously is the correct method for dilation of air. As far as I know, no device exists that can do that. If we would be able to test that we might find out that that movement is incorrect as well, as a matter of fact, I expect that movement to be similarly incorrect. If we for example could construct an airtight metal sphere that could grow, then probably that movement would create a lot of tension as well. A turbomolecular pump is a device that is used to create a high vacuum, not with a plunger but with a rapidly spinning turbine blades. It appears that its working principle is not dilative morphing, nor sequential morphing. So there are still things that need to be discovered, and things that need to be understood.
With sequential morphing, it is always one vortex that morphs into one other vortex. With dilative morphing, it are sometimes two or more vortices that combine into one single larger vortex. The bells in the third cycle are formed by a combination of several vortices from the second cycle. But so far it appears that all vortices that dilate from the first cycle dilate towards one single vortex in the second cycle. The example above shows several vortices from the first cycle that eventually dilate towards one single larger bell. Here it are two revolutes, two pylons and one bulb. I am not sure if one bulb is correct. I am not sure if two pylons can connect to one bulb. A more logical solution might be that the bulb should be a binary bulb, connected with a bridge, an exobar. That binary bridge would then dilate to form the core of the bell.
Shifting
Morphing is caused by a change of angle of movement of a wave that travels in the onefield. When we observe any form of morphing that takes place here on our planet earth, this change of angle of movement, which is a form of contraction or expansion, is caused by movement and forces that act locally in our environment that we inhabit. But there is also a type of morphing called shifting. Here also the gradual change of a vortex's appearance changes from one position in the sequence to the next. Shifting is not caused by local forces at the location of the vortex, shifting is caused by movement of the observer. It is the morphing of vortices that takes place far away, caused by our own movement here at where we are in our space and time.
In all the mesocyclic scale observations that we see here on earth where an object is dragged along with the flow movement of a vortex, the object is not pushed or pulled into the higher or lower dimensions. This is simply because the object, or even a small particle like a dust grain, is too large to be influenced by the larger vortex in that way. But this process does happen, it does happen all around us with particles that are much smaller than that, and that cannot be seen with the naked eye.
For example, when a piece of paper gets pulled in by a tornado, in such a way that it's lifted into the air and spun around the axis of the tornado a few times, then that piece of paper does not move towards the higher dimensions (tornado makes an expansive movement). We simply know that because that piece of paper does not change in appearance, no change in its material properties occurs, and it does not disappear. The tornado is way too small to be able to do that.
What is able to do that is a vortex of astronomical size. Our earth moves within in a solar system that is hold together by the gravity of our sun. The gravitational field of our sun is a huge vortex that is large enough to pull our entire earth towards the lower dimensions. Our earth is like a giant spaceship that is constantly moving towards the lower dimensions. When we move towards the lower dimensions, we do not see ourselves contract. We are unaware of this because from our reference frame, this process of contraction does not happen for us. For us it appears that objects in the universe around are expanding. It appears as if not us, but the objects in the universe around us are constantly moving towards the higher dimensions. And this movement is called shifting.
It appears as if not us are moving downwards, but that the objects in the universe around us are constantly shifting towards the higher dimensions.
Not all, but some of the movement that we see in the universe around us, as seen from our location on the earth, is caused by shifting. We are however limited in what movement we are able to see with our current technology, because vortices that are astronomical in size move very slowly. It is not completely certain how galaxies move, how they morph, and how they flow. The best thing we can do now is study the movement of similar type of vortices here on earth, and make estimations for the differences that result from the difference in size and the medium in which the movement occurs. But because the movement of galaxies can not be observed, we also don't know if sequential shifting looks the same as sequential morphing. It could be that shifting gives a different effect in how one shape changes into another. One that we haven't been able to observe yet.
The same happens on a microcyclic scale. One example is a vacuum created by expanding air. The volume inside a vacuum chamber becomes higher dimensional on a mesocyclic scale by the expanding movement that is made to create to vacuum. The air dilates. As a reaction, the particles on a microcyclic scale become lower dimensional, they contract. This type of contraction is called dedilation. Because of the contraction, and thus decrease in size, of all microcyclic vortices within the volume of the vacuum chamber, these vortices are no longer detectable. Particles are no longer detectable.
We will also introduce the terms 'upward shifting' and 'downward shifting'. Upward shifting is the equivalent of upward morphing. Downward shifting is the equivalent of downward morphing. The first is expansion, the second is contraction. When a vortex is not shifted we say that that vortex is unshifted, which is the equivalent of unmorphed.
More Examples of Morphing
If you've read all the pages until this page, then you've already seen a considerate number of examples of morphing. In most cases, sequential morphing. In the pages that are about to come you'll also see plenty of examples. Understanding morphing helps us understand the world better. It helps us understand the world on a mesocyclic scale, macrocyclic scale and microcyclic scale. It helps us understand chemical reactions, and changes in material properties of matter that occur over time. It also helps us to find more puzzle pieces of the transformation sequence, because of the logical order of the sequence. Whenever you see a vortex, there's a considerate change that you're looking at a vortex that is an intermediate state between two vortex types. From all the information that I've presented so far you should in many cases be able to tell which vortex or morphology of vortices you're looking at, and at what approximate position within the transformation sequence that vortex is located.
| All content on this site that is authored by Peter.A.Venis is licensed under the Creative Commons CC BY 4.0 license, unless otherwise mentioned. Most pages on this website also include material from other authors, under different licenses. Both the author's names and the licenses are mentioned in the file names whenever this information is known and can be provided. The presence of work from other authors on this website does not necessarily imply that those authors endorse the contents of this website. |
| A word that is often used on this website is the word 'vortex'. Many sources describe a vortex as a movement in a fluid that has a rotational flow. Yet many of the vortices that I describe on this website do not show a visible rotational flow. I took the liberty of using the word vortex for describing a phenomenon that had not been understood before, one that links together rotational and non-rotational movements. Even a movement in a straight line can in some cases be categorized as a vortex, if it is known that that movement is created by certain identical conditions. So keep in mind that the word 'vortex', within the context of the infinity-theory, has not the exact same meaning as other sources describe. |